相対論への招待（その３５） - 相対性理論を学びたい人のために

　現在２０２０年３月２９日０時０６分である。

麻友「寝てないじゃない」

私「ローレンツ変換のことが、気になって、眠れなくなってしまったんだ。明日は、予定がない。眠くなるまで、書くことにするよ」

麻友「眠くなったら、寝るのよ」

私「うん」

私「さて、問題になっていたのは、 ${(b \cosh t', b \sinh t')}$ という点が、双曲線

$\frac{x^2}{b^2}-\frac{y^2}{b^2}=1$

上の点で、 ${t'}$ が、パラメーターだということだった」

麻友「ストップ。パラメーターって何？」

私「ああ、説明してなかったね。 ${x}$ と、 ${y}$ という変数があるとき、必ずしも、 ${y}$ が、 ${y=f(x)}$ と表されるとは、限らない。こういうとき、パラメーター（媒介変数（ばいかいへんすう）ともいう） ${t}$ などを用いて、 ${x=f(t)}$ 、 ${y=g(t)}$ などと、それぞれを、表せることがある。このように使われる、 ${t}$ などを、パラメーターと言うんだ」

麻友「ああ、なるほど」

若菜「お父さんにしては、説明が遅かったですね」

私「実例で、慣れてもらおうと、思ったんだ」

結弦「一応、新しい言葉は、説明してよ」

私「分かった」

私「３月１６日から、『麻友６７』の、ノートで、３３ページ目から、計算していて、３月２７日に使い切ってしまった。それで、もう昨日だが、３月２８日に、『麻友６８』のノートに書き始めた。その決意文、

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

２０２０．３．２８　１５：０３：５６「

　ローレンツ変換と戦う２人の言葉

麻友「もう十分時間もかけたのに、どうしてローレンツ変換が導けないの？」

私「どうしても、しっくりこない部分があるんだ。もうちょっと時間をくれない？」

麻友「太郎さんの完璧主義ももの凄いわね」

　　　　　　　　　　　　　　　　　　　言葉終

　　　　　　　　　　　　　　　」２０２０．３．２８　１５：１３：２２

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

麻友「さあ、始めてよ」

私「スキャン原稿・・・

　ここまで書いて、２時半頃寝た。

　さて、８時５３分起き、母のところへ、生活費を受け取りに行って、買い物して帰ってきて、書き始める。

　現在２０２０年３月２９日１１時３３分である。

私「スキャン原稿８枚目を、用意した」

f:id:PASTORALE:20200329113816j:plain

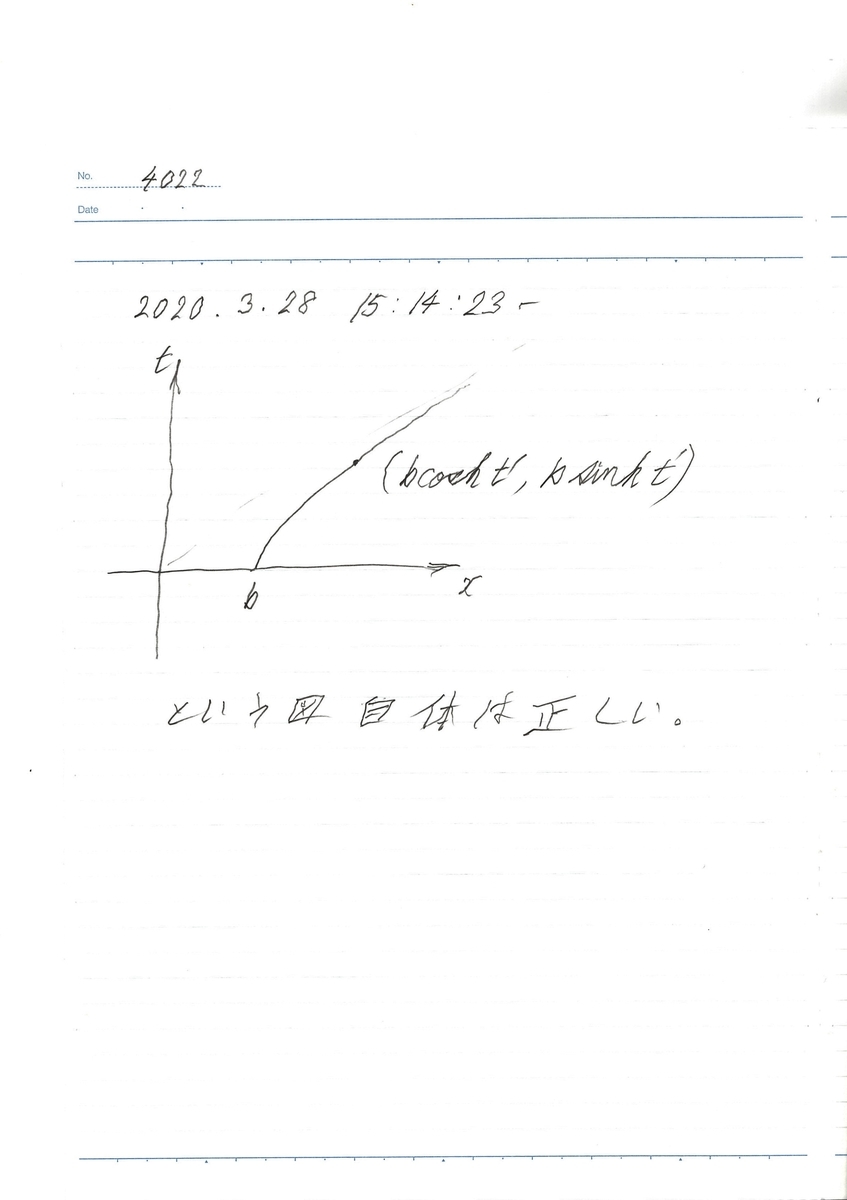
麻友「これを、確認したのね」

若菜「 ${(x,t)=(b \cosh t',b \sinh t')}$ が、双曲線、

$\frac{x^2}{b^2}-\frac{t^2}{b^2}=1$

上の点であることは、『相対論への招待（その２６）』で、お母さんが、確かめましたね。ただ、あのときは、この図の、 ${t}$ が、 ${y}$ で、 ${t'}$ が、 ${t}$ でしたけど」

私「そうだな。あのときは、この図の、 ${t'}$ が、動いている麻友さんの時間、つまり固有時間だ、というような、書きっぷりだった」

結弦「違うの？」

私「結局、ここで、ボタンを掛け違えたために、私の頭の中の計算が、全部狂ってしまった」

若菜「本当は、どうだったんですか？」

私「これを、読んで、分かるかどうか、心許ないけど、計算を見せる。

$d \tau =\sqrt{dt^2-dx^2-dy^2-dz^2}$

が、固有時間の定義だった。 ${\tau}$ は、ギリシャ文字のタウね。これが、動いている人の感じる時間だ、というのは、ローレンツ変換を、導けば、分かることだ。今は、導けたとして、計算してみる。この結果を、ローレンツ変換の導出には使わないから、循環論法には、ならない」

麻友「大変な計算？」

私「何をやっているかだけ、分かってもらえれば、いい。まず、 ${y}$ 軸方向、 ${z}$ 軸方向には、動いていないので、 ${dy=0,dz=0}$ 、よって、

$d \tau =\sqrt{dt^2-dx^2}$

分母、分子に、 ${dt'^2}$ をかけて、

$d \tau =\sqrt{\biggl(\frac{dt^2}{dt'^2}-\frac{dx^2}{dt'^2} \biggr)dt'^2}$

微分できる形に持っていって、

$d \tau =\sqrt{\biggl(\frac{dt}{dt'} \biggr)^2-\biggl(\frac{dx}{dt'} \biggr)^2}dt'$

${(x,t)=(b \cosh t',b \sinh t')}$ を代入して、

$d \tau =\sqrt{\biggl(\frac{d}{dt'}b \sinh t' \biggr)^2-\biggl(\frac{d}{dt'} b \cosh t' \biggr)^2}dt'$

微分して

$d \tau =\sqrt{(b \cosh t')^2-(b \sinh t')^2}dt'$

いつもの形に持っていって、

$d \tau =b \sqrt{ \cosh^2 t'- \sinh^2 t'}dt'$

${\cosh^2 x-\sinh^2 x=1}$ だったから、

$d \tau =b dt'$

結局、

${\tau =b t'}$

である」

麻友「ごめん。最後の所だけ、分からない」

私「ああ、実は、積分定数を、省略したんだ。本当は、

${\tau =b t' + C}$

もあり得る。 ${C}$ は、任意の定数ね。なぜなら、両辺を、 ${t'}$ で、微分すれば、定数の微分はゼロで、

$\frac{d \tau}{dt'}=b$

でしょ。だから、両辺に ${dt'}$ を、かけて、

$d \tau =b dt'$

となって、合ってるでしょ」

麻友「それは、・・・」

若菜「つまり、お父さんが、一番簡単な形の、微分方程式を解いたということですね」

結弦「僕たち、『微分・積分入門』、どんどん読んでいるんだよ。ところで、お父さん、躓いた原因の、

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

麻友「あの、ハイパボリックサインや、ハイパボリックコサインは、この場合、何なの？」

私「 $\frac{v}{c} = \beta =\tanh t'$ だよ。だから、初めに種明かししますの精神にのっとるなら、

$\sqrt{1-\frac{v^2}{c^2}} = \sqrt{1-\beta^2} =\sqrt{1-\tanh^2 t'}=\sqrt{1-\frac{\sinh^2 t'}{\cosh^2 t'}}$

$=\sqrt{\frac{\cosh^2 t' -\sinh^2 t'}{\cosh^2 t'}}=\sqrt{\frac{1}{\cosh^2 t'}}=\frac{1}{\cosh t'}$

が、ローレンツ因子・・・

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
（『相対論への招待（その３２）』より）

なんだけど、これ間違いだったの？」

私「あのとき、私の頭では、 ${t'}$ は、固有時間ということになっていた。だから、何かおかしい、と思って、計算を止めたんだけど、 ${t'}$ を、ただのパラメーターと思うのなら、間違いではなかった。あくまでも、 ${\tau=bt'}$ が、固有時間だと置き直せば良い」

麻友「じゃあ、間違いは、なかったの？」

私「いや、４枚目のスキャン原稿で、

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　 ${t'}$ 系と ${t''}$ 系は、 ${A}$ ， ${B}$ の点で、 ${t}$ 系から見て、同じ速度。 ${t'}$ 系， ${t''}$ 系から見て、 ${A}$ ， ${B}$ は、同時刻。

　コノライン上の点は、加速系で同時刻。

　最初からそのときまで、ずっと同時刻。

　相対論では、同時刻ラインは傾くので、

などとはならない。

f:id:PASTORALE:20180317105742j:plain

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

とあるが、

『 ${t'}$ 系と ${t''}$ 系は、 ${A}$ ， ${B}$ の点で、 ${t}$ 系から見て、同じ速度』

は、良いが、

『 ${t'}$ 系， ${t''}$ 系から見て、 ${A}$ ， ${B}$ は、同時刻』

は、間違い、かも知れない」

麻友「大丈夫なの？」

私「なんとかするよ。麻友さんとの愛がかかってる」

麻友「待ってるわ」

私「じゃあ、おやすみ」

若菜・結弦「おやすみなさーい」

麻友「おやすみ」

　現在２０２０年３月２９日２１時５０分である。おしまい。